
Cet été au Québec, le ciel se prenant pour la mer projetant sur le sol des marées de pluies incessantes toutes les secondes, le mot "cône" fait davantage penser à ceci :

Rares sont les élus qui savent qu'un cône, un vrai, a pour ainsi dire la forme d'un sablier qui refuse de laisser passer le temps.

On appelle conique les figures obtenues en tranchant un cône de révolution à l'aide d'une guillotine.
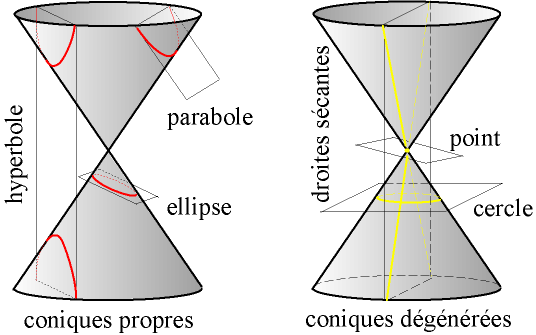
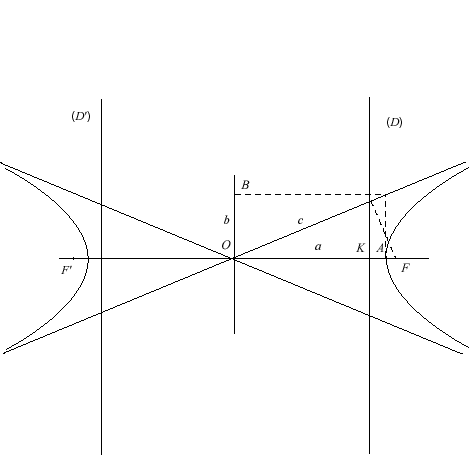
On y trouve l'hyperbole.
Hyperbole... du grec hyper, qui veut dire au-delà et bole, de ballein, jeter. L'hyperbole, c'est jeter au-delà, c'est l'excès, l'exagération.
On peut définir mathématiquement l'hyperbole de plusieurs façons. Le site de Mathcurve étant une référence incontestée, une mine de renseignements essentiels que nul matheux non nul ignore, il serait ici aussi inutile de répéter son contenu que de tenter de le reprendre de manière plus concise, complète et précise.
L'équation générale de l'hyperbole (centrée à l'origine) est :

(Source : Mathcurve)
Lorsque a=b, nous avons affaire à des hyperboles équilatères (équi = égal, latère = côté). Ses asymptotes sont alors perpendiculaires, la figure est plus agréable à regarder...

... et plus facile à manipuler !

Lorsque l'on regarde l'hyperbole équilatère, la figure précédente, puisque les asymptotes sont perpendiculaires, on pourrait les prendre comme repère, c'est-à-dire faire faire une rotation de 45° à notre hyperbole pour obtenir ceci :

La rotation d'une figure peut être obtenue de façon banale à l'aide d'une matrice de rotation.

Escamotons les détails d'algèbre matricielle sur lesquels nous pourrons revenir plus tard, nous obtenons, lorsque l'on fait tourner notre hyperbole équilatère, la transformation suivante (que vous pouvez lire en diagonale !) :

Ici pour un angle de 45°, on a un triangle isocèle, donc deux jambes égales de 1/√2.
On continue donc avec ce cas particulier :

Si vous avez l'œil, vous constaterez que les deux éléments de la matrice de droite sont identiques sauf pour le signe entre les termes. Les multiplier apportera nécessairement quelque chose de joli (eh oui, ça sert aussi à ça la factorisation).

Oh oh, mais qu'est-ce que cette chose ? y = k/x ? Mais c'est une fonction rationnelle !
Mais ce n'est pas tout...
Sachant que l'intégrale définie correspond à l'aire sous la courbe (théorème fondamental du calcul), quelle est l'intégrale de la fonction k/x ? Eh oui, le logarithme naturel (qui avant Euler s'appelait d'ailleurs logarithme hyperbolique).
C'est donc dire, enfants du secondaire, que l'hyperbole, la fonction rationnelle et les logarithmes qui vous font tant souffrir et qui vous semblent si éloignés ont le potentiel de s'unir... pour le meilleur et pour le pire... et en rendant la chose un peu plus complexe, ils sont même liés aux fonctions trigonométriques. Eh oui, dans l'excès de l'hyperbole, toutte se tient.
9 commentaires
Dans les temps anciens et reculés, un prof de maths, le seul à mes yeux..., m'avait expliqué que le calcul d'un volume n'était en fait qu'une intégrale...
Je serais bien incapable de l'expliquer aujourd'hui, mais sans doute pourras-tu me rafraichir la mémoire ?
;o)
Histoire d'occuper tes vacances...
Miss; tu connais les Coneheads?
Gaël, ton prof de maths était un vrai matheux. Il est vrai que le calcul d'un volume n'est qu'une intégrale (enfin, toute une !), cependant, dans la vraie vie, à part les matheux, les calculs de volume sont rarement faits avec des intégrales. C'est que pour intégrer, il faut une intégrande (la fonction que l'on intègre) et il est rare que les volumes "naturels" occupent ces formes-là... et pour les autres, il existe des formules toutes faites. Enfin, tu conviendras avec moi qu'il est bien chic de calculer le volume d'un cube en intégrant, mais tellement plus rapide d'élever la longueur d'une arête au cube !
Prof masqué, je connaissais l'affiche des Coneheads, je viens d'aller voir la bande annonce... à la prochaine pluie, j'oserai le film... peut-être...
Je ne comprends rien aux équations, évidemment.
Ma spécialité serait plutôt les cornets et les hyperboles de la langue française, mais je suis toujours tellement fascinée par la manière donc tu fais les liens entre tout sujet et les mathématiques. Brillant!
Miss; prochane pluie, ça veut dire demain... Je ne suis pas sûr, concernant le film. Mais il y a un côté un peu absurde, slapstick qui pourrait te plaire.
Pour celui qui n'est pas très fort (ou simplement avancé) en math et qui lie se blogue, j'ai effectué quelques démarches avant d'arriver sur ce blogue pour prouver qu'une hyperbole ayant une boîte de même dimension (équilatère) est en fait une fonction rationnelle tourner.
Pour y arrivé j'ai fonctionné à l'aide de triangle sembable et de droites rencontrant l'hyperbole en des lieux précis, et à l'aide des essais (non malheureusement je n'ai pas utilisé uniquement l'aglèbre) j'ai pu remarqué que les points prévus à l'aide de l'hyperbole était en fait les points réels de la fonction rationnelle. J'ai ensuite chercher une démarche un peu plus scientifique sur internet. (C'est là que j'ai découvert ce formidable blogue)
Une formule toute simple permet de trouver, à partir de l'hyperbole équilatère centré à l'origine, la fonction rationnelle correspondant:
a1(au carré)=2*a2
Où a1=a de l'hyperbole
et a2=a de la fonction rationnelle
Math,
Hum... je t'aimais bien toi, mais là, je t'adore !!!
Si jamais ça te tente, j'aimerais bien publier ici ta démarche. Il nous faudrait trouver un moyen de mettre tout ça en forme, soit en image (jpg) ou alors en texte... Enfin, je te laisse y penser, je ne veux pas te brusquer non plus, mais on néglige trop ces approches intuitives auxquels on ne pense plus dès qu'on a les "bons outils".
J'ai fait un document word à partir de ma démarche, seulement je n'ai pas trouver ton adresse e-mail dans l'information de ton compte google. Si possible me l'envoyer ( je ne vais certainement pas la vendre à quelques compagnies de spamming que ce soit...)
Il n'y a pas d'image non plus, malheureusement je n'ai pas vraiment de logiciel pour se faire et paint irait un peu mal...
Math,
Aprendi mucho
Publier un commentaire